este tipo de duibujo (en este caso el dibujo tecnico ) tine que hacerse los poligonos
Una forma poligonal es una porción de superficie, contenida en el interior de la figura resultante de unir varios puntos del plano no alineados, de tal modo, que ninguna de las líneas de unión pase por más de dos de ellos a la vez.
De toda forma arquitectónica podemos hacer abstracción para obtener su forma poligonal, pero también lo podríamos hacer de cualquier forma vegetal, animal, o simplemente de un objeto de uso cotidiano.
Dada la infinidad de formas poligonales con las que nos podemos encontrar, se hace necesario hacer una distinción entre la forma poligonal y el polígono que la envuelve con el fin de facilitar su utilización en el Diseño.
entre ellas son:
cuadrado
l polígono regular
rombo
trapecio trapezoide
pentágono
hexágono
etc.
EL CUADRADO
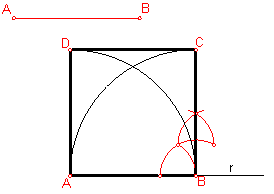
Fig. 86
Sea el lado ab:
Sobre una recta r cualquiera, llevamos el valor del lado dado.
Por el extremo A y B, levantamos dos perpendiculares.
Haciendo centro en A y B traza dos arcos hasta que corten a las perpendiculares anteriores, obteniendo los vértices C y D.
b) Cuadrado regular, dada la diagonal. Fig. 87.
La diagonal del cuadrado coincide con el radio de la circunferencia circunscrita.
Con centro en O, trazamos la circunferencia circunscrita.
Seguidamente, trazamos sus diámetros ortogonales obteniendo los puntos A, B, C, D.
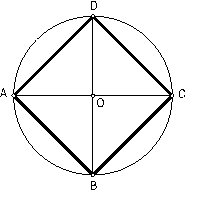
Fig. 87
Uniendo los puntos A, B, C, D, tenemos la solución.
1.2. Rectángulo
a) Construcción de un rectángulo dada el lado y la diagonal. Fig. 88.
Bastará con construir dos triángulos rectángulos, dada la hipotenusa y un lado.
Sobre una recta r, llevamos el valor del lado AB.
Por el extremo B levantamos una perpendicular.
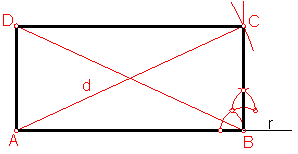
Fig. 88
Haciendo centro en Ay con radio el valor de la diagonal d, trazamos un arco, obteniendo el vértice C.
Repetimos la operación en el punto A.
1.3. Rombo
a) Construcción de un rombo dada la diagonal y un lado. Fig. 89.
Sea el lado AB y la diagonal d:
Será preciso construir el triángulo isósceles dado por la diagonal y el lado. ( dos datos).
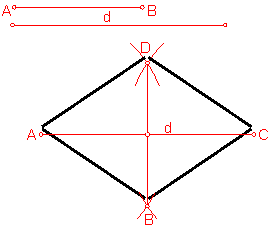
Fig. 89
Trazamos la mediatriz de la diagonal dada d.
Haciendo centro en los extremos A y B trazamos dos arcos con el valor AB que determinan los vértices C yD.
1.4. Romboide
a) Construcción de un romboide dado dos lados y la diagonal. Fig. 90.
Sean los lados AB y BC, y la diagonal d.
Como la diagonal divide al romboide en dos triángulos escálenos. Bastará con construir dicho triángulo conociendo tres de lados.
Sobre una recta llevamos el valor del lado AB.
Con centro en A trazamos un arco de radio el valor de la diagonal d.
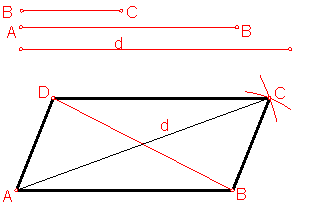
Fig, 90
Con centro en B, repetimos la operación con el valor del lado BC, obteniendo el vértice C.
La unión de ABC determina uno de los triángulos. Repitiendo la operación tendremos el otro.
b) Construcción de un romboide dado dos lados y el ángulo que forman. Fig. 91
Sea el ángulo A y los lados AB y BC:
Bastará con construir un triángulo escaleno conociendo dos lados y el ángulo comprendido.
Sobre una recta r y en su extremo, construimos el ángulo A.
Con centro en A y radio AB trazamos un arco punto B.
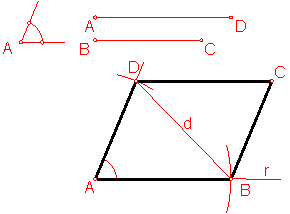
Fig. 91
Con centro en A y radio AD trazamos otro arco, punto D.
La unión de ABD, determina uno de los triángulos.
El otro se halla de forma similar.
c) Construcción de un romboide dado dos lados a y b y el ángulo menor de las diagonales que vale 75º ( opuesto al lado dado a). Fig. 92.
Resolveremos el ejercicio por medio de arco capaz, teniendo en cuenta que el lado b es paralelo a la mediana ma del triángulo formado por el lado a yel ángulo que forman las diagonales.
Sobre una recta llevamos el lado a.
Construimos el arco capaz de 75º.
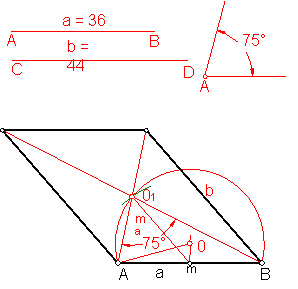
Fig. 92
Con centro en m y radio la mitad del lado b, (mediana del triangulo buscado) trazamos un arco que determina el punto O1.
La unión de A, B, O1, nos determina el triangulo que forma las diagonales y el lado a.
Prolongamos la diagonal A O1. y con centro en By radio b, trazamos un arco, obteniendo teniendo el vértice C.
Mediante paralelas completamos el ejercicio.
1.5. Trapecio
a) Trapecio rectángulo conociendo la base mayor la altura y el ángulo
que forma dicha base con el lado. Fig. 93.
Sea b la base mayor, h la altura y α el ángulo que forma la base mayor con el lado b.
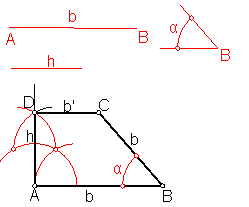
Fig. 93
Sobre una recta llevamos la base mayor b.
En el extremo A levantamos una perpendicular h.
Llevamos sobre dicha perpendicular el valor h dado, puntoD.
En el extremo B, trasladamos por medio del compás el ángulo α.
Por D trazamos una paralela a la base mayor, obteniendo el vértice C.
b) Trapecio rectángulo conociendo la base mayor b la altura h y la diagonal d. Fig. 94.
Sea b la base mayor, h la altura y d la diagonal.
Sobre una recta llevamos la base mayor b.
En el extremo A levantamos una perpendicular h.
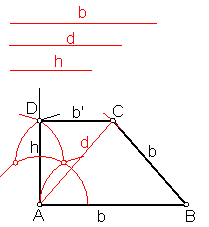
Fig. 94
Llevamos sobre dicha perpendicular el valor h dado, punto D.
Por D trazamos una paralela b’ a la base mayor b.
Haciendo centro en A y con el valor de la diagonal d trazamos un arco que corta a b’ en C.
c)Trapecio isósceles dada la base mayor b la media bm y la altura h. Fig. 95.
Sea b la base mayor y bm la media y h la altura.
Hallamos la mediatriz de b y a partir de 3 llevamos h.
Hallamos la mediatriz de h.
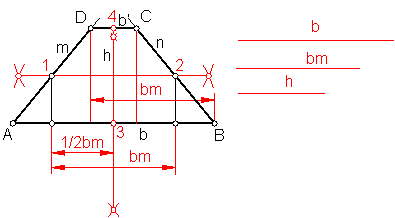
Fig. 95
Llevamos a partir de 3 a cada lado ½ bm y levantamos dos perpendiculares hasta que corte a la mediatriz en los puntos 1-2
Unimos A con 1 y B con 2
A partir de A y B llevamos el valor de la bm.
Levantamos dos perpendiculares que cortarán a las rectas m y nen los puntos C y D.
d) Trapecio escaleno dadas las dos bases b y b’ y los dos ángulos adyacentes a la base mayor. Fig. 96.
Sean b la base mayor, b’ la menor, y A y B los ángulos adyacentes a la base mayor.
Llevamos sobre una recta el valor de la base mayor b.
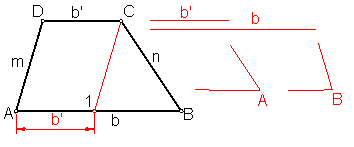
Fig. 96
En sus extremos construimos por medio del compás los ángulos dados A y B
A partir de A llevamos el valor de la base menor.
Por el punto 1 trazamos una paralela a la recta mque corta a la n en C.
La unión de D y C nos determina el trapecio.
e) Trapezoide dados los cuatro lados y la altura correspondiente a uno de ellos. Fig. 97.
Sean los lados a, b, c y d y la altura ha.
Sobre una recta llevamos el valor del lado a.
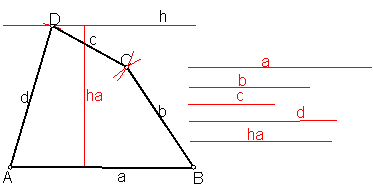
Fig. 97
En un punto cualquiera de ella, trazamos una recta perpendicular, llevando el valor correspondiente a la altura ha.
Con centro en A, y radio el valor del lado d, trazamos un arco que cortará a la paralela h en el punto D.
Con radio c, y haciendo centro en C, trazamos un arco.
Con centro en B y radio B, trazamos otro arco. Ambos se cortan en el vértice C. La unión de todos ellos nos determinan el trapezoide.
2) Polígonos
2.1. Construcción de polígonos dado el radio de la circunferencia circunscrita
El triángulo y el cuadrado han sido visto con anterioridad, por tanto comenzaremos por aquellos superiores a 4 lados.
a) Hexágono regular dado el radio de la circunferencia circunscrita Fig. 98.
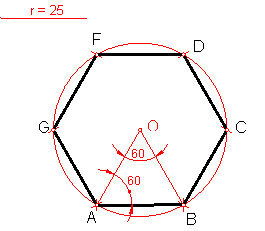
Fig. 98
Tendremos en cuanta que el valor del lado es igual al radio r de la circunferencia.
b) Pentágono regular dado el radio de la
circunferencia circunscrita. ( procedimiento exacto). Fig. 99.
Con centro en O, trazamos la circunferencia
circunscrita y seguidamente sus diámetros
ortogonales A, B, C, D,
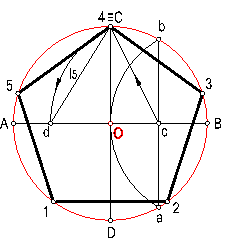
Fig. 99
Hallamos la mediatriz del radio, punto c.
Hacemos centro en c y con radio cC, trazamos
el arco Cd.
La distancia dC, será L5, lado del pentágono.
c) Heptágono regular dado el radio de la circunferencia circunscrita. (procedimiento aproximado). Fig.100.
Con centro en O, trazamos la circunferencia
circunscrita y seguidamente sus diámetros
No hay comentarios:
Publicar un comentario